En 1990, à l’occasion de la « journée de la Terre », la municipalité de New York décida de fermer la 42ème rue à la circulation. Cette rue étant l’une des plus animées de Manhattan, on pensait que cette fermeture ne manquerait pas de ralentir la circulation et de provoquer des embouteillages supplémentaires. C’est le contraire qui se passa: le fait de fermer la 42ème rue rendit la circulation plus fluide! C’était l’une des premières fois où l’on voyait se réaliser « en vrai » un phénomène mis en évidence de manière théorique en 1968 par un universitaire allemand: le paradoxe de Braess.
Dès 1968, le mathématicien Dietrich Braess montrait que le fait d’ajouter un itinéraire de délestage peut provoquer des congestions et allonger les temps de parcours au lieu de les raccourcir. Cette proposition peut sembler pour le moins audacieuse, en particulier pour tous les automobilistes qui râlent contre les embouteillages et qui réclament la création de nouvelles routes!
Le « bon sens » automobilistique veut en effet que tout problème récurrent d’embouteillage et de congestion trouve sa solution dans la mise en place d’infrastructures nouvelles.
Alors comment est-il possible qu’en créant de nouvelles routes ou de nouvelles rues, on arrive à dégrader les conditions de circulation?
Le paradoxe de Braess (1) s’énonce ainsi :
« Etant donnés le nombre de véhicules partant de chaque point d’un réseau routier, et leur destination, on cherche à estimer la distribution du flot de circulation. Le fait qu’une voie soit préférable à une autre dépend non seulement de la qualité de la voie, mais également de la densité du flux. Si chaque conducteur emprunte le chemin qui lui paraît le plus favorable, les temps de trajet résultant ne sont pas nécessairement les plus faibles. De plus (cela est montré par un exemple), une extension du réseau routier peut entraîner une redistribution du réseau qui résulte en des temps de trajet plus longs. »
Un petit modèle pour comprendre
Un petit modèle explique mieux qu’un long discours ce paradoxe de Braess (2).
Supposez que vous cherchiez à vous déplacer d’une ville (A) à une autre (D) plus vite possible. Deux itinéraires s’offrent à vous, l’un passant par B, l’autre passant par C, chacun composé d’un bout de nationale et d’une route départementale. Le temps de parcours sur les nationales est de 45 minutes quelque soit la circulation. Par contre, comme il y a des feux sur les départementales, le temps de parcours dépend du nombre de voitures X qui l’emprunte: il vaut par exemple X/100 minutes.
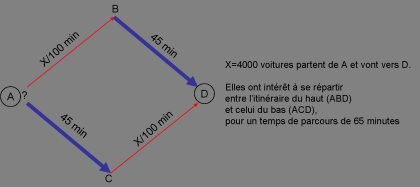
Supposons qu’il y ait 4000 voitures souhaitant passer de A à D. Si elles prennent toutes le trajet du haut (ABD) elles mettront 85 minutes. Idem si elles prennent toutes le trajet du bas. La situation optimale sera celle où le trafic s’équilibre entre les deux trajets. Le temps de parcours sera alors de 45 +2000/100 = 65 minutes.
Pour désengorger la circulation, on construit une voie ultra-rapide reliant B et C, dont le temps de parcours est négligeable quelque soit le nombre de véhicules qui l’emprunte (pas très réaliste mais bon c’est un modèle!). Avec cette voie rapide, le temps de parcours entre A et B devrait raccourcir, or c’est l’inverse qui se produit:
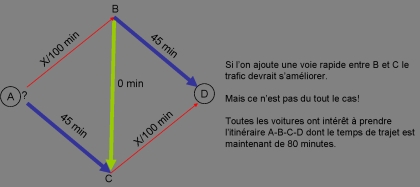
Le meilleur trajet pour les 4000 voitures est maintenant (ABCD): départementale – voie rapide – départementale et le temps de trajet passe ainsi de 65 minutes à 80 minutes! Essayez vous même: si une des voitures prenait un autre itinéraire, son trajet serait rallongé de 5 minutes (45+40=85).
L’explication la plus évidente de ce paradoxe a été faite par la mathématicien Étienne Ghys, dans un article intitulé « Le prix de l’anarchie » (3): ce qui rend possible le paradoxe de Braess, c’est le comportement foncièrement égoïste des automobilistes. Chaque automobiliste choisit sa route comme il le souhaite et tous les conducteurs essayent d’optimiser leurs itinéraires, y compris en tentant d’anticiper ce que feront les autres!
Un paradoxe… paradoxal
Ce qui rend le paradoxe de Braess… paradoxal, c’est qu’on associe instinctivement la circulation routière à un « flot » de voitures, donc soumis aux mêmes principes d’écoulements que les liquides ou les gaz. Or dans un écoulement fluide, plus il y a de chemins possibles, plus l’écoulement est facile: aucun plombier n’a encore vu de système dans lequel ajouter un tuyau d’évacuation boucherait des éviers.
La raison profonde de cette différence entre nous et les molécules d’eau, implicite dans nos modèles, semble venir du fait que nous cherchons à rejoindre notre but le plus vite possible, compte tenu de ce que les autres font (ou ont intérêt à faire). Dès qu’on spécule de la sorte, nos déplacements collectifs échappent aux règles de la mécanique des fluides et fabriquent des problèmes inédits.
Une fréquence… fréquente
Le paradoxe de Braess est-il fréquent ? Pour un réseau aléatoire, Valiant et Roughgarden (4) montrent que le paradoxe de Braess se produit avec une probabilité presque sûre si le nombre de villes est grand.
Depuis la découverte du paradoxe en 1968, de nombreux cas réels ont vérifié son hypothèse:
- A Seoul (Corée du Sud), une amélioration du trafic autour de la ville a été observée lorsqu’une voie rapide a été supprimée lors du projet de restauration de Cheonggyecheon (5).
– A Stuttgart (Allemagne), après des investissements sur le réseau routier en 1969, la situation ne s’est pas améliorée jusqu’à ce qu’une section de route nouvellement construite soit à nouveau fermée au trafic.
- En 1990, la fermeture de la 42e rue à New York a réduit la congestion dans cette zone (6).
– En 2008, Youn, Gastner et Jeong ont pointé du doigt des itinéraires spécifiques à Boston, New York et Londres où cela pouvait effectivement être le cas, et désigné des routes qui pourraient être fermées pour réduire les temps de trajets.
- En 2011, suite à la fermeture de l’Interstate 405, l’absence d’un fort trafic dans une large zone est potentiellement considérée comme l’exemple le plus récent du paradoxe de Braess à l’œuvre.
Des conséquences… conséquentes
L’existence de tels phénomènes contre-intuitifs interroge avec perplexité sur la capacité à mener des politiques publiques de déplacements visant effectivement à l’amélioration d’un système.
Imaginons un cas concret (7), à savoir une ville connaissant d’importantes difficultés de trafic pour entrer et sortir de la ville.
Arrive un ingénieur en trafic qui pointe un carrefour particulièrement congestionné et propose qu’en le dénivellant, c’est à dire en construisant un autopont, la circulation s’en trouvera fluidifiée. Ce message, tout intuitif, est simple à faire passer auprès des élus et de la population: « construisons une infrastructure et la situation s’améliorera« .
Pourtant, dans l’état des connaissances actuelles, au regard des données disponibles, et à l’aune de phénomènes comme ceux expliqués par Braess, il est impossible d’affirmer que la réalisation (coûteuse) d’un autopont améliorera quoique ce soit. Il est même tout à fait possible que la construction d’un autopont détériore les conditions de circulation sur le carrefour et augmente encore les difficultés de trafic pour entrer et sortir de la ville.
Mais il est beaucoup plus aisé pour un élu d’expliquer à ses concitoyens qu’il réglera leur difficulté par la création d’un autopont, que de leur expliquer que cet aménagement risque au contraire de rendre leurs déplacements plus difficiles et qu’il convient de privilégier des politiques de report modal (de la voiture vers un autre mode).
Dans le premier cas, le lien est direct et parle à nos sens (surtout à travers les comparaisons classiques de mécanique des fluides), dans l’autre cas, cela prend du courage et de l’énergie pour expliquer, illustrer, faire comprendre, convaincre, car l’évidence immédiate a disparu.
En tout état de cause, il est tout de même intéressant de savoir que le fait de transformer par exemple une rue en rue piétonne peut parfois fluidifier la circulation…
Image en tête d’article: Roadshow par Hubert Blanz, 2007.
Notes
(1) Le Paradoxe de Braess sur Wikipédia
(2) Le Paradoxe de Braess sur Webinet
(3) Le prix de l’anarchie, Ghys E., Images des Mathématiques, 06/07/2009.
(4) Braess’s Paradox in Large Random Graphs, G. Valiant and T. Roughgarden, , EC’06, 17/11/2009.
(5) Détruire les autoroutes permet d’améliorer le trafic et d’embellir votre ville, Marcel Robert, Carfree France, 13/07/2009.
(6) What if They Closed 42d Street and Nobody Noticed?, Gina Kolata, The New York Times, 25/12/1990.
(7) Paradoxe de Braess, intérêt collectif, phénomènes contre-intuitifs et politiques publiques, Pensées urbaines, 29/09/2009






Merci de rappeler de temps en temps ce phénomène (une piqure de rappel fait parfois du bien), qui est, en effet, contre intuitif. Néanmoins, l’explication reste théorique, et l’article cité en référence (7) me semble le plus pertinent car il montre des exemples plus concrets pour convaincre les non matheux qui ne veulent pas faire un effort d’abstraction, d’une part, et qui resteraient sceptiques sur ce concept théorique.
j’ai du relire 3 fois le petit modèle mathématique mais ça se tient…par contre je ne comprends pas trop le X (nbre de voitures)/100min. S’il n’ y a qu’une seule voiture qui emprunte la route elle ne mettra pas 1 centième de minute (soit 0,6 sec) pour aller de A à B! Ou alors ça marche avec une fourchette de véhicules?
c’est une facon de modéliser une petite route.
En gros, un modèle plus fin dirait par exemple :
jusque 500 voitures, le temps de trajet est constant car la route n’est pas saturée : par exemple 50min
et à partir de 500, la route commence à saturer, et le temps devient proportionnel au nombre de voiture : genre NombreVoitures/10… Donc 600 voitures –> 60 min, 1000 voitures–>100min etc.
pour une grande route : il a posé un temps constant car elle peut accueillir un gros nombre de voitures sans saturer…. (par exemple 6000 et au max, il en passait 4000 dans l’exemple)
Je ne connaissais pas, très intéressant et malheureusement vrai.
Mais le problème n’est pas limité à l’automobile, il est présent avec quasiment tous les modes de déplacement à mon avis. De même qu’avec la marche…
Pas de chance, Ragnarok, mais celà ne marche pas, à pied (sic) :
celà marche (enfin… justement, non, celà bouchonne…) en voiture,
car elles peuvent choisir des routes à 130-110-90-70-50-45-30-20
donc elles cherchent à utiliser le plus possible les voies rapides… quitte à faire un détour (aller vers le sud, pour rejoindre l autoroute de contournement qui nous mènera au nord… pour contourner la ville; puis, une fois au nord, redescendre dans des rues à 45km/h au sud (trajet fait, afin de ne pas partir plein nord, dans le centre-ville bouché)).
à pied.. il n’y a pas de voies exprès (le métro/le bus peuvent jouer le rôle ?)
donc tu ne fais pas un détours de 5km pour marcher à 4km/h sur un grand boulevard, afin de ne pas marcher à 4km/h dans une ruelle étroite*
(sauf si tu as peur de marcher seul(e), le soir d’une nuit sans lune et de panne d’éclairage public, dans la ruelle).
* bon… pour des préférences de vitrines, de magasins ou autre, une rue commerçante peut avoir plus de marcheurs qu’une ruelle qui n a que des maisons/immeubles de logement, où seuls les habitants (et leurs amis) ont une raison d’aller.
@Raghnarok : comment veux tu qu’avec la marche on puisse construire des « voies rapides » pour piétons? En gros, le temps est toujours constant avec des piétons donc la construction d’un nouveau troncon ne peut raccourcir un temps de trajet (ou très peu). En plus la surfréquentation d’un itinéraire ralentit rarement les piétons (à part pendant les très saintes soldes)
à vélo, ca pourrait devenir vrai, s’il y a congestion cycliste et si tu considères qu’il y a des routes sur lesquels tu roules bcp plus vite que d’autres…. C’est plutot ultra rare.
En fait ce modèle est particulièrement adapté à la voiture, car la circulation ralentit avec le nombre d’usagés qui n’est pas limité (c’est d’ailleurs le vrai problème des embouteillages : il faudrait limiter le nombre d’usagers au dimensionnement des routes, comme on limite le nb de passagers de trains).
Pour les autres moyens c’est un peu faux : avion, bateau aucun souci meme en cas de forte affluence (à part un peu de cohue en aerogare/port). Train, le réseau est dimensionné et le nombre de places limitées par les réservations. C’est partiellement vrai dans le cas des troncons surfréquentés par les trains qui tombent plus facilement en panne, ce qui allonge le temps de trajet.
metro : ca parait applicable. Une nouvelle ligne ‘rapide’ deviendra surfréquentée, ce qui allonge les temps d’attente aux stations et donc le temps de trajet.
Vous voyez d’autres cas applicables?
Hello,
je crois que cela s’applique aussi aux piétons, mais plutôt dans une entrée/sortie vers une correspondance de métro par exemple.
il me semble avoir vu ça sur une étude des flux de piétons, ou les gens essaient d’anticiper comment vont se déplacer leurs « voisins », et les blocages (bouchons/ralentissement) qui en résultent.
Pour les piétons, il y a de la gestion de foule… qui peut-etre, s apparente de loin à l effet Braess.
Exemple de gestion de foule :
devant une sortie de métro/devant une sortie d urgence d’un batiment (en cas de feu, d alerte à la fuite de gaz, de..),
soit on met une grande porte
-> tous le monde sort par la grande porte, et elle bouchonne.
Cas particulier de l évacuation d’un bâtiment : une fois les gens sortis, ils s arrêtent assez vite -> un amas se forme à quelque mètres de la sortie… l espace laissé libre entre la sortie et l amas se comble au fur et à mesure, si bien qu’après un moment, tout est bouché (les 1ers arrivés, ayant de l espace devant eux, donc n étant pas particulierement serrés, ne voient pas de raison d aller plus loin).
La solution partielle a été trouvé :
diviser le flux :
-> plusieurs petites sorties
ou (moins bien, mais si on ne peut pas changer le nombre de sorties) un poteau après la grande sortie (séparation du flux en 2 : à droite ou à gauche du poteau : au lieu d aller tout droit en sortant, les gens dévient à respectivement à droite/gauche après le poteau)
Dans l’évacuation du bâtiments, les 1ers sortis continuent à s’arrêter trop tôt, à ne pas marcher jusqu’au « point de RDV ».
Mais comme il n’y a plus que la moitié/le tiers/le quart* de gens qui arrivent derrière eux, celà pose moins de pb.
* en supposant une division parfaitement homogène, ce qui n est -bien sûr- pas le cas.
Le coup du poteau s’apparente à l ‘effet Braess, par sa contre-intuitivité :
on rajoute un obstacle…
celà fluidifie,et accélère le temps d évacuation du batiment.
Effectivement, après réflexion je pense qu’à pieds le problème ne peut pas vraiment arriver, par contre à vélo il y a bien des chances que ça arrive.
Sur les transports « publics », imaginons une nouvelle voie de métro, hyper rapide et fréquente, si tout le monde l’utilise il faut attendre plusieurs passages pour pouvoir y entrer, ce qui pose aussi un problème, alors que les petites voies périphériques peuvent être vides. À mon avis toujours, pas vraiment fait d’études à ce sujet.
Bien vu pour la gestion des foules dans les couloirs de metro et autres lieux événementiels. Concernant les études sur les réseaux de transports publics (métro par ex), des tas d’études existent sur « que se passe t il si cette station est en panne ? » , « comment se fait le report sur les autres stations etc. etc. »
Moi j’attends les voies rapides pour vélos avec impatience. je suis prêt à doubler mes distances de parcours!
Ce qui est intéressant avec le paradoxe de Braess, c’est de le mettre en relation avec des projets actuels. Dans ce cadre, la fermeture des voies sur berge à Paris pourrait en fait améliorer la circulation, malgré ce que dit la droite parisienne…
Moi j’ai un autre exempl de paradoxe de Braess à Paris;
j’ai habité toute mon enfance porte de gentilly, sur les maréchaux. A l’époque il y avait 4 voies pour les bagnoles (y compris les bus). Ca bouchonnait à mort tous les soirs; je me souviens qu’un jour j’avais mis plus d’une heure trente pour aller en PC (bus) jusqu’à la porte de saint cloud, pour ceux qui connaissent. Si bien que je préférais faire des détours énormes en métro pour aller plus vite aun Parc des Princes!
Puis il y a eu une voie de bus, et ça allait mieux même pour les voitures!
Et maintenant il y a une voie de tramway et une voie pour les vélos, il reste que deux voies pour les bagnoles, et ca roule beaucoup mieux!
Peut-être que quelqu’un d’averti ou du milieu de l’urbanisme pourrait faire un courrier « pro » sur ce paradoxe au cabinet d’étude pour le projet de fermeture de la voie sur berge de Paris. Ils n’ont peut-être pas imaginé qu’on pouvait démontrer que ce serait un « mieux » pour les automobilistes aussi. Toute la critique s’écroulerait d’un coup !
Ce raisonnement est typique d’un manque de prise en considération de la dimension spatiale du trajet et de l’ hypothèse absolument fantaisiste de poser que le temps de parcours entre B et C serait quasi nul, alors que la distance entre B et C est manifestement importante.
Par contre, la suppression d’une artère bouchée peut fluidifier le trafic tout comme cela se passe dans le corps humain où les vaisseaux capillaires, les petites rues permettent d’effacer les nœuds à problème, à condition que les autorités urbaines n’aient pas systématiquement cassé la fluidité dans ces artères secondaires en prenant des mesures destinées à ralentir le trafic en mettant une mi-longueur dans un sens et l’autre dans l’autre sens, en mettant des sens uniques successifs et non alternés dans les rues perpendiculaires, etc..
@ Nonmais
Casser la fluidité = ne pas transformer les centre-ville en autoroutes collées à des trottoirs = ralentir le flux de véhicules = avoir moins de morts.
Tout responsable des déplacements urbains VRAIMENT responsable, casse justement la fluidité, en créant des contournements autour de certains pâtés de maisons (au lieu d’avoir une ligne droite de la Place de X à la Place Y).
c.f. http://tinyurl.com/citymove
De même, tout maire d’un village sur un nationale, respectueux de ses concitoyens, place à l ‘entrée et à la sortie de son village un round point, pour que les camions (et voitures) ne traversent pas son village à 90 km/h.
(une utilisation vraiment utile du rond point)
En fait, les rond points cassent la vitesse, permettent d avoir moins de morts… mais, statistiquement, permettent aussi d avoir une moyenne plus élevée qu’une succession de feux verts et rouges… qui font freiner puis partir de 0 (on ralenti, avec un rond point, mais on roule quand même à 30, 40, 50, voire au-delà)
http://www.rtl.fr/actualites/transports/article/une-femme-et-sa-fille-de-11-ans-meurent-fauchees-par-une-voiture-a-paris-7751025008
Tiens, hier, une fillette de 11 ans et sa mère, ont été tuées par un chauffeur avec 0 points de permis, à Paris, sous les yeux du père-mari et de l’oncle-frère.
La fluidité était parfaite, à l’endroit où elles ont été tuées.
(sans ces piétons qui font tjrs chier, il aurait pû rouler encore plus vite, mais elles l’ont un peu ralenti)
Mais il n’y a pas que Paris, qui a droit à ses belles routes bien fluides :
dans le même temps, un garçon de 6 ans mourait, et son père était gravement blessé à Saint-Georges d’Oléron (Charente-Maritime)
[précision : il ne s’agit que d’une fraction réduite du nombres de morts sur la route, hier, en france.
rappel de la moyenne journalière française, de morts violentes directes par la route : 11]
La fluidité, choix de nos représentants dès l’époque de Pompidou, commence seulement à être -partiellement- remise en cause, mais il reste encore beaucoup de chemin à faire.
Ben pourquoi ce serait fantaisiste de dire que BC est quasi nul ? ABD et ACD peuvent être 2 trajets quasi parallèles.
Ce que tu appelle casser la fluidité c’est fait plutôt pour « empêcher le transit » ou le « trafic malin ». Si ça fini par être plus avantageux de passer par des petites rues, les voitures le feront, au grand dam des riverains. Donc je trouve tout à fait normal qu’on fasse passer les voitures par les grands axes et qu’on ne facilite pas la traversée de quartiers résidentiels ou de centre-villes aux voitures.
Et en général, mais bizarrement beaucoup de gens pensent le contraire, on créé des sens unique pour fluidifier le trafic. Ben oui 2 grosses voitures qui se croisent dans une rue pas très large, ça ralentie, voire ça bouchonne si il y en a beaucoup. Si on passe en sens unique, les voitures peuvent rouler plus vite. C’est pour ça que les associations de riverains et de cyclistes intelligentes militent contre les sens-uniques : car plus de vitesse = plus d’accidents. Mais comme il faut quand même garder des sens uniques pour la raison évoquée au paragraphe précédent, la solution la plus évidente est le double sens cyclable.
Excellente remarque Apanivore. D’ailleurs les contre sens cyclables (ou SUL pour nos amis belges) ont prouvé par expérience qu’ils ne sont pas source d’accidents malgré ce qu’en pensent et disent les bagnolards. Pas de blessé grave ni mort à déplorer dans ces voies.
Et puis meme dans les grandes villes ou les petits vélos sont dessinés sur le sol tous les 10m, et les sens interdits SAUF VELOS sont à jour, il reste des automodébilistes agressifs (pleonasme) qui n’ont toujours pas compris et qui ralent « y a des trottoirs pour ca, c…… ». Alors on rappelle ici que les trottoirs sont autorisés aux « cyclistes » de moins de 8 ans! (c’était ma minute complainte)
http://www.leparisien.fr/paris-75/voies-sur-berge-a-paris-les-automobilistes-se-rebiffent-11-09-2012-2159822.php
Pour 4 malheureux feux, ça chouine dans les habitacles. (C’est plutôt les piétons et les cyclistes qui pourraient râler face au peu d’ambition – euphémisme – de l’aménagement réalisé)
Pourtant la préfecture de police ose affirmer que le temps de parcours sur la rive droite aux heures de pointe a légèrement baissé depuis la rentrée. Paradoxe de Braess illustré, CQFD.